Name:Lan Vu
Date:
Course ID: CSC 5682
Semester:Fall 2007
Simulation of the MIU system
that shows the variety of strings that can be produced starting from any
well formed axiom, such as MI.
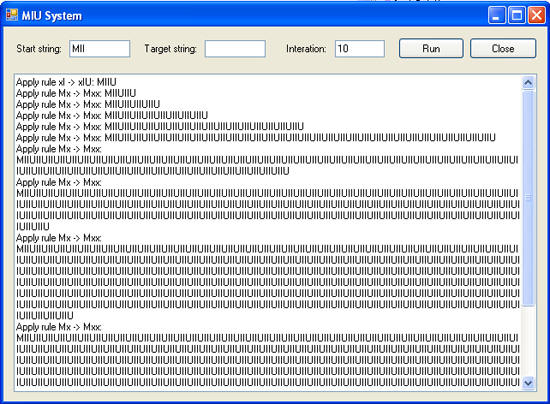
The computer simulation of MIU System is shown in below interface. It is implemented in C++ language NET Framework 2.0.
Click here for full source code
of this program.

1.
Why is the MIU System called typographical?
The MIU
System is called typographical because this system uses its typographical
rules for deduction to produce variety of strings from basic symbol M, I,
and U.
Deduction using these rules in
the
MIU
System is same with
some operations
found in a
typographical
system defined in GEB:
(1)
Reading and recognizing any of a finite set of symbol
(2)
Writing down any symbol belonging to that set
(3)
Copying any of those symbols from one place to another
(4)
Easing any of those symbol
(5)
Checking to see whether one symbol is the same as another
(6)
Keeping and using a list of previous generated theorems
2.
How does the MIU System use deduction?
Starting
from any well formed axiom, such as MI, MIU system uses its rules for
deduction. After each time of applying rules on current theorems, the system
creates new strings derived from given axioms
and they
become new theorems. Deduction continues until the expected theorem is
proved.
3.
Does the MIU System use induction in any way?
Explain.
The MIU
system does not use induction in any way because the theorem to be proved is
a specific one, not in general form. Moreover, this expected theorem may not
be proved by applying such rules of MIU System.
4.
Explain any realistic interpretation of the
symbols, or strings of symbols, in the MIU System.
I find
no realistic interpretation of the symbols, or strings of symbols, in the
MIU System because they have no meaning.
5.
Explain how conflict resolution is implemented
in your simulation.
During
the deduction process, rules applied by prior order rule 1
à
rule 2
à
rule 3
à
rule 4. If rule 1 doesn’t work, rule 2 is tried.
6.
Does your implementation of the MIU System use
forward or backward chaining?
Explain.
My
implementation of the MIU System use forward chaining. With a start string,
the system will apply MIU System’s rules to create new strings until the
target string is found.
7.
The MU Puzzle: Given only the axiom MI, is MU deducible in the MIU System?
The answer is no.
8.
Provide a convincing argument that MU is, or is not, deducible by the MIU
System given only the axiom MI to start with.
According to Wikipedia,
MU is
not deducible by the MIU System given only the axiom MI to start with.None
of the rules allows us to create a string whose total number of
Is is a multiple of
three, except by starting with another such string. Since we can only start
with MI which contains
one I, we can never
produce such a string. In particular, we can never produce a string
containing no Is, such as
MU.
To see this, notice that the only rule which allows us to add "I"s to our
string is rule 2, which will double the number of "I"s in the string, while
the only rule which allows us to remove "I"s from our string is rule 3,
which will remove 3 "I"s from the string.
Thus, the total number of "I"s in a string must be of the form 2a
– 3b, where
a
and
b
are constants, and
i
is the number of "I"s in our axiom.
9.
Explain the relationship between the results of your
simulation and automated theorem proving.
For example, how would the computer know if it
was getting closer to proving the theorem or just spinning its wheels?
In my
stimulation, goal search are expanded all branches of tree, so all possible
rules applied to produce new strings. Search process will stop if target is
found or limitation of search level is reach. I don’t determine how getting
closer to proving the theorem.
References
1. The
GEB book: http://tal.forum2.org/geb
2.
Course Materials.
3. See
the web references on the Links page of course website.
4.
http://en.wikipedia.org/wiki/MU_puzzle (gives a solution to the MU puzzle).