Assignment #3: Planning
-
Name:Lan Vu
-
Date:10/1/2007
-
Course ID: CSC 5682
-
Semester:Fall 2007
|
For this
assignment we simulate a particular Blocks World Planning Problem,
called EBW (Elementary Blocks World). This "toy" problem provides
us with a simple scenario for testing ideas about expert, or
rule-based, approaches to automated problem solving.
Problem
Description (EBW)
There
are n blocks (labeled A, B, C, ...) in any number of stacks on a
table. You are given an initial state and a goal state. You are
to find the fewest moves that move the blocks from the initial state
into the goal state. Assume that the initial state is on one
table and the goal state is to be constructed on a separate table
(all blocks have to be moved at least once). The rules are:
-
can only
move one block at a time.
-
can only
grab a block that is on the top of a stack (can't pull a block
out from within a stack).
-
once you
grab a block you can either put it on another block (hopefully
building the goal state) or put it down on the table.
The objective
is to find a method that finds a path, or "plan", that moves the
initial state into the goal state in the fewest moves.
For this
assignment we will build a computer simulation of this
problem and apply various heuristics to create solutions.
Example
 |
1. Find the shortest path for the example
given above. If there is more than one shortest path, present them all.
Shortest path 1
-
Put D down on the table.
-
Put B down on the table.
-
Place E in its goal state position.
-
Place B in its goal state position.
-
Place F in its goal state position.
-
Place C in its goal state position.
-
Put A down on the table.
-
Place G in its goal state position.
-
Place A in its goal state position.
-
Place D in its goal state position.
Shortest path 2
-
Put D down on the table.
-
Put B on F.
-
Place E in its goal state position.
-
Place B in its goal state position.
-
Place F in its goal state position.
-
Place C in its goal state position.
-
Put A down on the table.
-
Place G in its goal state position.
-
Place A in its goal state position.
-
Place D in its goal state position.
Shortest path 3
-
Put D down on the table.
-
Put B on D.
-
Place E in its goal state position.
-
Place B in its goal state position.
-
Place F in its goal state position.
-
Place C in its goal state position.
-
Put A down on the table.
-
Place G in its goal state position.
-
Place A in its goal state position.
-
Place D in its goal state position.
Three above paths take 10 “moves”
2.
Show that the following heuristic will create valid, but not necessarily
optimal, solutions: Use these rules: If any available block (any block at
the top of a stack in the initial state) can be moved directly to its final
position in the goal state then does it. If not, then take the block on the
top of the largest stack and move it to the table (if there are two largest
stacks then break ties by using the first stack as counted left to right).
Iterate in this fashion until the goal state is achieved. Show that this
method can produce an optimal solution in some cases, bust suboptimal in
others (give an example of each).
In the best case, we can build the goal
state in just n steps because all blocks can be moved directly to
their final position. In the worst case, if there is no block being moved
directly to its final position in first n-1 iterations, all blocks
will be put down on the table and then they are moved to the goal state. So,
this heuristic will create valid, solutions.
This method can produce an optimal solution
in some cases. For example:
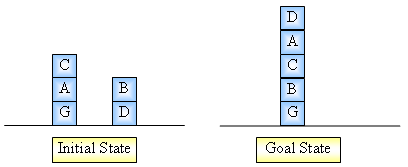
Apply the above heuristic we have a
following solution and it’s also an optimal one:
-
Put C down on the table.
-
Put A down on the table.
-
Place G in its goal state
position.
-
Place B in its goal state
position.
-
Place C in its goal state
position.
-
Place A in its goal state
position.
-
Place D in its goal state
position.
(It took 7 steps)
This method can produce suboptimal in
others. For example:
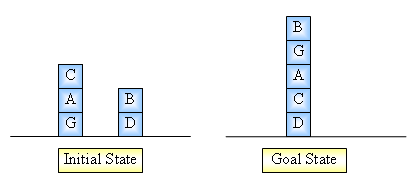
Apply the above heuristic we have a
following solution but it’s not an optimal one.
-
Put C down on the table.
-
Put A down on the table.
-
Put B down on the table.
-
Place D in its goal state
position.
-
Place C in its goal state
position.
-
Place A in its goal state
position.
-
Place G in its goal state
position.
-
Place B in its goal state
position.
(It took 8 steps)
In this case, the optimal solution should
be:
-
Put B down on the table.
-
Place D in its goal state
position.
-
Place C in its goal state
position.
-
Place A in its goal state
position.
-
Place G in its goal state
position.
-
Place B in its goal state
position.
(It took 6 steps)
3. Explain why, in an optimal solution, no
block more should be moved more than twice.
The problem always has one clear method of
finding a path that is to move all the blocks to the table and then build
the goal state. In this solution, each block just needs to be moved less
than or equal to twice. Because an optimal solution must be better than this
one, no block more should be moved more than twice in an optimal solution.
4.
Explain why finding the shortest path reduces to decide which blocks will be
moved twice and which ones will be moved only once.
In finding the shortest path, if there is
any block that can be move directly to its final position, we will do that
and it does not take us time to decide whether that block is moved twice and
once. Therefore, this also helps to reduces deciding which blocks will be
moved twice and which ones will be moved only once.
5.
Explain how the concept of "deadlock" applies to this problem. Give
examples.
In
this problem, the concept of "deadlock" introduced by [1]:
The
set of blocks {b1, b2,….bp} is
deadlocked in the state S if there is a set of blocks {d1, d2,….dp}
such that the following three conditions hold:
-
In S, bi is
above di for i = 1,2,….,p
-
In G, bi is
above di+1 for i = 1,2,….,p-1, and
bp is above d1
-
In S, none of b1, b2,….bp
are in their final positions (if p>1 then the other two conditions
entail this condition)
An illustration of the definition of
deadlock
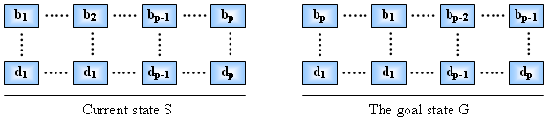
For example:

The set of blocks {C, B} is
deadlocked because B is in C’s way and C is in B’s
way.
6. Create a computer simulation of this
blocks world problem (graphical display is extra credit). Implement the
heuristics described above: H1: all blocks go to the table, then moved into
final positions; H2: described in 2 above. Invent a better heuristic if you
can.
The
computer simulation of this blocks world problem is shown in below
interface. I used language C# Framework 2.0 to implement this demo. It allows creating
a random problem. The problem may be
solve with Heuristic 1 or Heuristic 2. Its solution is shown in graphical images (each image
is a step of that solution).
The source code of this demo.

An example of using this demo:
When clicking "Generate an EBW
problem" with parameter value: Number of block = 5 and Number of Column
= 2, you may have such below problem:
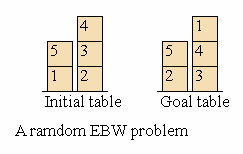
Then you may use Heuristic 1 or
Heuristic 2 to find the solution by clicking a suitable button:
The solution with Heuristic 1
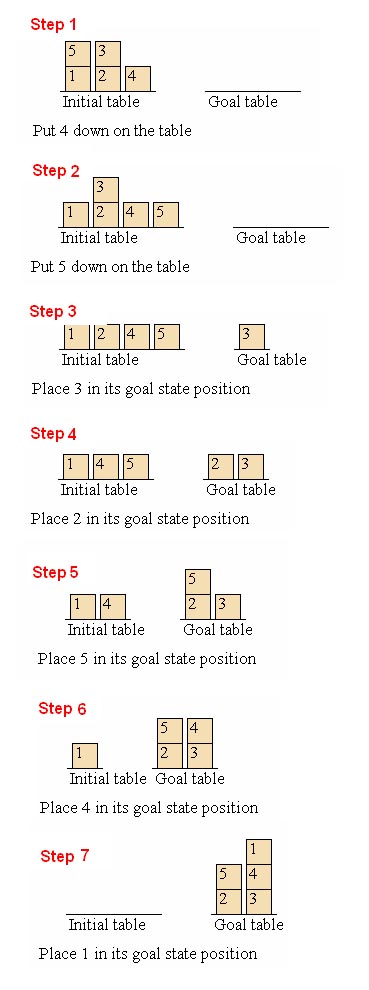
should be shown as following image (it took 8 steps):

The solution with Heuristic 2
should be shown as following image (it took 7 steps):
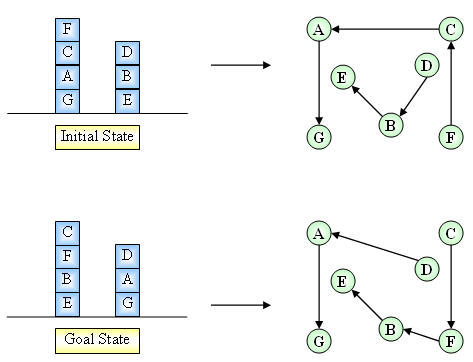
7. a) Create a graphical representation of
this problem using a directed graph with nodes that correspond to the blocks
and arcs that indicate a constraint created by the initial or goal state
configurations.
I use Hasse diagram introduced in [1] to
represent this problem. Consider the graph H(F) whose nodes are the blocks,
and having an arc from block B to block C if and only if B
is on C.
b) Research the Feedback Arch Set problem.
This problem boils down to finding the fewest arcs to remove from a directed
graph that will make it acyclic (no more cycles), and it is known to be NP
complete. Explain how EBW reduces to the Feedback Arc Set problem, and
thereby show that EBW is NP complete. (This is actually difficult, so I am
not expecting perfect answers, just some rationale -- make an attempt to
understand the Feedback Arc Set problem, and then try to tie it together
with the graphical representation you came up with in part a). All of this
shows that this simple blocks world planning problem is of equal complexity
to the better-known traveling salesman problem.
Definition
of a Feedback Arc Set
from Wikipedia
:
In
graph theory, a
directed graph may contain
directed cycles, a one-way loop of edges. In some applications, such
cycles are undesirable, and we wish to eliminate them and obtain a
directed acyclic graph (DAG). One way to do this is simply to drop edges
from the graph to break the cycles. A feedback arc set (FAS)
is a set of edges which, when removed from the graph, leave a DAG. Put
another way, it's a set containing at least one edge of every cycle in the
graph.
The
proof that EBW PLAN is NP-hard
According to [1], for each digraph (V,E),
an EBW problem B, such that finding a set of k blocks that resolves all
deadlocks in B corresponds to finding a Feedback Arc Set of size k in (V,E).
But the dificulty of finding a small Feedback Arc Set makes the Feedback Arc
Set problem NP-hard. Thus, the difficulty of finding a small set of blocks
that resolves all deadlocks makes EBW Plan NP-hard.

- "On the
Complexity of Blocks-World Planning"
by: Naresh Gupta, Dana S. Nauz Artificial Intelligence, 56(2-3):223 -
254, August 1992
- Wikipedia for
basic definitions
.










