Name:Lan Vu
Date:10/20/2006
Course ID: CSC 5682
Semester:Fall 2007
A.1. Wikipedia search: Bayesian Network
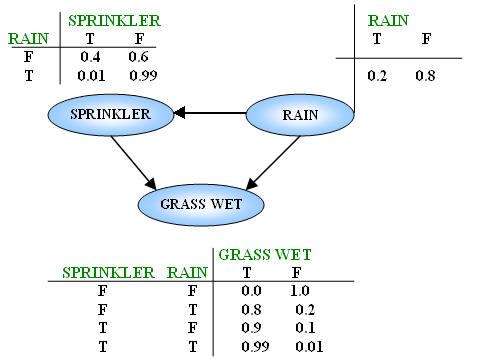
Sprinkler Example
For clearer understanding about Bayesian Network’s definitions and concepts, let take a look at below Sprinkler example.

This is a very simple Bayesian Network with 3 nodes standing for grass, sprinkler, rain and 3 arcs showing relationships between them.
In this model, grass, sprinkler, rain are three variables that have two possible values T (for true) and F (for false). Grass is wet because of two reasons: either the sprinkler is on or it's raining and the use of the sprinkler depends on rain. With these relationships, the joint probability function is:
P(G,S,R) = P(G | S,R)P(S | R)P(R) (*)
G = Grass wet, S = Sprinkler, and R = Rain,
Suppose that you want to know "What is the probability that it is raining in case of the grass is wet?". To answer this question, P(R=T|G=T) should be calculated by applying conditional probability formula:
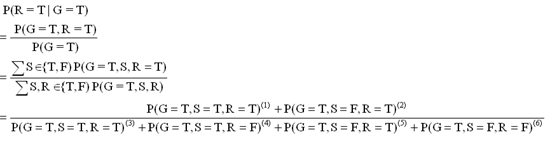
Apply (*) to this problem:
(1) = (3) = P(G=T,S=T,R=T) = P(G=T|S=T,R=T) P(S=T|R=T) P(R=T)= 0.99*0.01*0.2 = 0.00198
(2) = (5) = P(G=T,S=F,R=T) = P(G=T|S=F,R=T) P(S=F|R=T) P(R=T) = 0.8*0.99*0.2 = 0.1584
(4) = P(G=T,S=T,R=F) = P(G=T|S=T,R=F) P(S=T|R=F) P(R=F) = 0.9*0.4*0.8 = 0.288
(6) = P(G=T,S=F,R=F) = P(G=T|S=F,R=F) P(S=F|R=F) P(R=F) = 0.0*0.6*0.8 = 0
So we have:

In the same way, if you want to know "What is the probability that the sprinkler is on, given the grass is not wet?", you should calculate P(S=T|G=F) by applying conditional probability formula:

Apply (*) to this problem:
(7) = (9) = P(G=F,S=T,R=T) = P(G=F|S=T,R=T) P(S=T|R=T) P(R=T) = 0.01*0.01*0.2 = 0.0002
(8) = (10) = P(G=F,S=T,R=F) = P(G=F|S=T,R=F) P(S=T|R=F) P(R=F) = 0.1*0.4*0.8 = 0.032
(11) = P(G=F,S=F,R=T) = P(G=F|S=F,R=T) P(S=F|R=T) P(R=T) = 0.2*0.99*0.2 = 0.0396
(12) = P(G=F,S=F,R=F) = P(G=F|S=F,R=F) P(S=F|R=F) P(R=F) = 1.0*0.6*0.8 = 0.48
The result is:
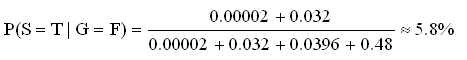
What if I suppose that there is no relationship between the use of the sprinkler and rain? Certainly, we will have another Bayesian Network as following image:
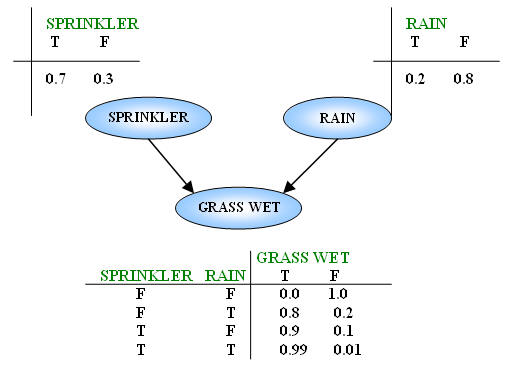
The joint probability function should be revised:
P(G,S,R) = P(G | S,R) P(S) P(R) (**)
P(S|R) in (*) is replaced by P(S) in (**) because Sprinkler doesn’t depend on rain anymore and it has no parent.
In this case, there is a little change in the answer for the above question: "What is the probability that it is raining in case of the grass is wet?".
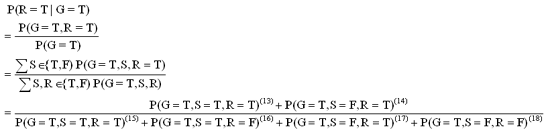
Apply (**) to this problem:
(13) = (15) = P(G=T,S=T,R=T) = P(G=T|S=T,R=T) P(S=T) P(R=T)= 0.99*0.7*0.2 = 0.1386
(14) = (17) = P(G=T,S=F,R=T) = P(G=T|S=F,R=T) P(S=F) P(R=T) = 0.8*0.3*0.2 = 0.048
(16) = P(G=T,S=T,R=F) = P(G=T|S=T,R=F) P(S=T) P(R=F) = 0.9*0.7*0.8 = 0.504
(18) = P(G=T,S=F,R=F) = P(G=T|S=F,R=F) P(S=F) P(R=F) = 0.0*0.3*0.8 = 0
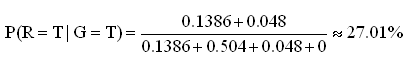
A.2. Wikipedia search: Bayes' Theorem
Cookies
Suppose there are two bowls full of cookies. Bowl #1 has 10 chocolate chip cookies and 30 plain cookies, while bowl #2 has 20 of each. Fred picks a bowl at random, and then picks a cookie at random. We may assume there is no reason to believe Fred treats one bowl differently from another, likewise for the cookies. The cookie turns out to be a plain one. How probable is it that Fred picked it out of bowl #1?
Assume that the event A is that Fred picked bowl #1 and the event B is that Fred picked a plain cookie.
In this problem, what we want to know is "what’s the probability that Fred picked bowl #1, given that he has a plain cookie?” or P(A|B). Because the event B relates to the event A, Bayes' theorem will help us find the answer.
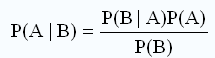
P(A) or the probability that Fred picked bowl #1 regardless of any other information. Because there are only two bowls, the chance that one of them is picked is equal. So, P(A) = 0.5
P(B) or the probability of getting a plain cookie regardless of any information on the bowls. This case is similar to the situation that all cookies in two bowls are mixed together in bowl X and Fred picks one cookie from bowl X. There are totally 80 cookies in bowl X (40 from bowl#1 and 40 from bowl#2). Among them, there are 50 plain cookies (= 30 + 20) and 30 chocolate chip cookies (=10+20). So, P(B)= 50/80 = 0.625
P(B|A), or the probability of getting a plain cookie given that Fred has selected bowl #1. From the problem statement, we know this is 0.75, since 30 out of 40 cookies in bowl #1 are plain.
=> P(A|B) = (0.75*0.5)/0.625 = 0.6
Drug testing
Bayes' theorem is useful in evaluating the result of drug tests. Suppose a certain drug test is 99% accurate, that is, the test will correctly identify a drug user as testing positive 99% of the time, and will correctly identify a non-user as testing negative 99% of the time. This would seem to be a relatively accurate test, but Bayes' theorem will reveal a potential flaw. Let's assume a corporation decides to test its employees for opium use, and 0.5% of the employees use the drug.
Assume that D is the event of being a drug user.
N indicates being a non-user.
+ is the event of a positive drug test.
What we want to know is the probability that, given a positive drug test, an employee is actually a drug user or P(D|+). According to Bayes' theorem, we have:
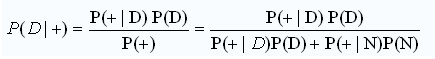
P(D) = 0.005 since 0.5% of the employees use the drug.
P(N) = 1-P(D) = 0.995.
P(+|D) = 0.99 since the test is 99% accurate.
P(+|N) = 0.01, since the test will produce a false positive for 1% of non-users.
P(+) = 0.015 or 1.5%, which found by adding the probability that the test will produce a true positive result in the event of drug use (= 99% x 0.5% = 0.495%) plus the probability that the test will produce a false positive in the event of non-drug use (= 1% x 99.5% = 0.995%).
P(D|+) = (0.99 * 0.005) / (0.99*0.005 + 0.01*0.995) = 0.3322 or 33.22%
Despite the high accuracy of the test, the probability that the employee is actually a drug user is only about 33%.
The Monty Hall problem
We are presented with three doors - red, green, and blue - one of which has a prize. We choose the red door, which is not opened until the presenter performs an action. The presenter who knows what door the prize is behind, and who must open a door, but is not permitted to open the door we have picked or the door with the prize, opens the green door and reveals that there is no prize behind it and subsequently asks if we wish to change our mind about our initial selection of red. What is the probability that the prize is behind the blue and red doors?
Let Ar, Ag, Ab are the events the prize is behind the red door, green door, and blue door. B is the event the presenter opens the green door regardless any other information.
What we want to know is the probability that the prize is behind the blue and red doors so P(Ar|B) and P(Ab|B) need to be computed with the Bayes’ formula:
P(Ai|B) = P(B|Ai)P(B)/ P(B|Ai) (i Î {r,g,b})
· P(Ar)=P(Ag)= P(Ab) = 1/3 since the ability appearing the event Ar, Ag, or Ab is equal.
· P(B) = 0.5 since there are only two door left after the author pick up the red one.
· P(B|Ar) = ½ since the prize is behind the red door, either the green or the blue can be picked randomly by presenter
· P(B|Ag) = 0 since the prize is behind the green door and the presenter is not permitted to open the door with the prize.
· P(B|Ab) = 1 since the red door has been picked, the blue door has with the prize, The presenter must open the green door.
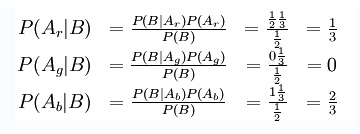
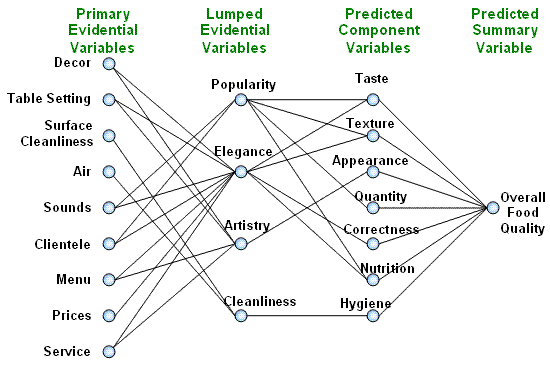
B.1: Explain the purpose of each node in the network.
The inference network as above image is designed for the estimate of the food quality. So, all nodes in this network are firstly used to supply this general purpose. They create the criteria and feature system which inference machine base on to make the conclusion about food quality. Because of their different roles in the whole inference process, they can be divided into 3 groups:
· Group 1 (input layer): including primary evidential variables (decor, table setting, surface cleanliness, air, sounds, clientele, menu, prices, and service). Each input variable can conceivably affect the evaluation of the food quality. These nodes play the role of receiving visual signals from user (traveler) to trigger the inference process of the network.
· Group 2 (Intermediate layers): including lumped evidential variables (popularity, elegance, artistry, cleanliness) and predicted component variables (taste, texture, appearance, quantity, correctness, nutrition, hygiene). These nodes appear in the network to simplify the relationships between inputs and output. The relationships between inputs and intermediates, between intermediates and other intermediates, and between intermediates and output(s) are easier to understand and describe than the relationship from inputs directly to output(s) [1]. The intermediate nodes receive the computed values of the input nodes or other intermediate nodes to update their confidence values which are used by output node to compute the final result.
· Group 3 (Output layer): including predicted summary variable (overall food quality). The information provided by predicted component variables is used to compute the final value of output node and the system will give user the result of food quality evaluation depending on this value.
B.2: Explain the numerical value associated with each node.
According to [1], each node of the inference network is represented by a symbol and its value, which is a structure. The structure has 6 components.
(defstruct node
name
prior-prob
prior-odds
current-prob
current-odds
arcs )
So, the numerical values associated with each node include:
· Prior probability P(X): the probability of node X regardless of any other information. This value will not change during the inference process.
· Prior odds O(X): can be calculated by using formula O(X) = P(X) /(1 - P(X))
· Current probability P(X|X’): the probability of node X given X’ where X’ are some observations that X is based on. This value will not be updated during the inference process.
· Current odds O(X|X’):
· Information of node’s incoming arcs. Two numerical values associated with each arc include l and l’
l is sufficiency coefficient
l’ is necessity coefficient
For example:
Nodes for the Primary Evidential Variables:
|
Name |
Prior probability |
Current probability |
Prior odds |
Information of incoming arcs (name l l’) |
|
Décor |
0.5 |
0.9 |
1 |
There is no incoming arc |
|
Table Setting |
0.5 |
0.8 |
1 |
|
|
Surface Cleanliness |
0.8 |
0.8 |
4 |
|
|
… |
|
|
|
Nodes for the Lumped Evidential Variables:
|
Name |
Prior probability |
Current probability |
Prior odds |
Information of incoming arcs (name l l’) |
|
Popularity |
0.5 |
0.6 |
1 |
Sounds 3.0 1.0 Clientele 1.0 0.24 |
|
Artistry |
0.5 |
0.9 |
1 |
Decor 1.0 0.5 Table setting 1.0 0.5 Menu 1.5 0.74 Service 1.0 0.5 |
|
… |
|
|
|
|
B.3: Explain how each node computes.
In an inference network the general format of an inference rule is "If E, then H," where E is the evidence and H is the hypothesis. In some cases, the evidence may be compound and instead of E we have E1, E2, ..., En. There Ei is the ith piece of evidence bearing on the hypothesis. E is in fact based on some observations E’.

Suppose that the node H need to be computed and it has k evidences
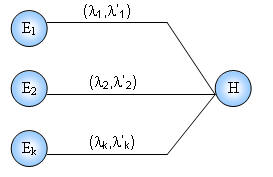
The current probability and current odds of node H are updated by following method:
Compute the current odds of H
Firstly, compute P(H|E’1), P(H|E’2) … P(H|E’k) in 3 steps:
1. Compute P(H|Ei) with the formula: P(H|Ei) = liO(H) / (1+liO(H))
2. Compute P(H|negEi) with the formula P(H|negEi) = l’i O(H) / (1+l’i O(H))
3. Compute from P(H|E’i) from P(Ei|E’i) using the function:
If P(Ei|E’i) <= P(Ei) then
P(H|E’i) = P(H|negEi) + P(Ei|E’i)*[P(H) - P(H|negEi)]/P(Ei)
Else
P(H|E’i) = P(H) + [ P(E|E’i) – P(Ei)]*[P(H|Ei) - P(H)]/[1-P(Ei)]
Secondly, compute the effective lambda values le1, le2, le3, …lek and the overall effective lambda lE
lei = O(H|E’i) / O(H) = P(H|E’i)/O(H)[1 - P(H|E’i)]
lE = le1 . le2 . le3 .….lek
Finally, compute Current odds of H: A = O(H) * lE
![]()
Current probability of H = A / (1+A)
For example: compute new values for popularity node among lumped evidential variables.

This node has 2 incoming nodes including sounds and clientele.
|
Computed Values |
Sounds (E1) à Popularity (H) |
Clientele (E2) à Popularity (H) |
|
P(Ei) |
0.5 |
0.5 |
|
P(Ei|E’i) |
0.5 |
0.9 |
|
P(H) |
0.5 |
|
|
O(H) = P(H)/(1-P(H)) |
1 |
|
|
P(H|Ei) = liO(H) / (1+liO(H)) |
0.75 |
0.5 |
|
P(H|negEi) = l’iO(H) / (1+l’iO(H)) |
0.5 |
0.19355 |
|
If P(Ei|E’i) <= P(Ei) then P(H|E’i) = P(H|negEi) + P(Ei|E’i)*[P(H) – P(H|negEi)]/P(Ei) Else P(H|E’i) = P(H) + [ P(E|E’i) – P(Ei)]*[P(H|Ei) – P(H)]/[1-P(Ei) |
0.5 |
0.5 |
|
lei = P(H|E’i)/O(H)[1 – P(H|E’i)] |
1 |
1 |
|
lE = le1 * le2
|
1 |
|
|
Current odds of popularity node: A = O(H) * lE |
1 |
|
|
Current probability of popularity node = A / (1+A) |
0.5 |
|
The new values for popularity node including:
· Current odds of popularity node = 1
· Current probability of popularity node = 0.5
References